Topics of Interest

The Jones Group

The University of East Anglia

Topics of particular interest include: excited state dynamics, light-molecule interactions, quantum dynamical models of ultrafast ultrabroadband 2D electronic spectroscopy, open quantum systems, and quantum information theory. These areas of interest are expanded below. Additionally, posters based on these areas of expertise can be found in Group Posters, as well as our publications, in Full Publications List.

Two-dimensional optical spectroscopy:

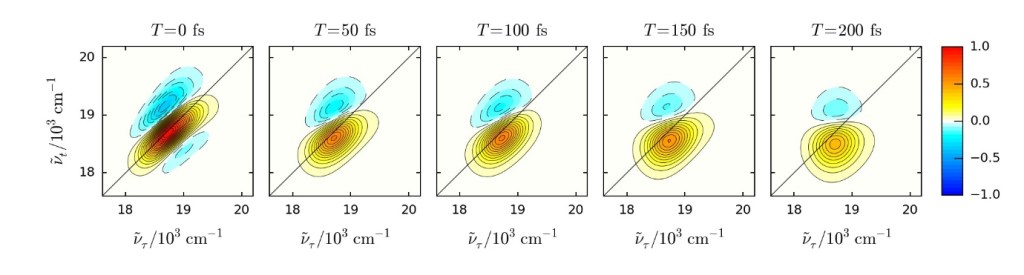
In our group we consider a wide range of light matter interactions. Many of our recent papers have involved convolving electric field signals into response functions. In particular, the third order response function for three waveforms is considered. Single interactions with each of the three fields can produce rephasing, or non-rephasing signals dependent on the sign of each constituent wavevector. These signals result in oscillating coherences and static peaks within a two-dimensional electronic spectrum as a consequence of different constituent Liouville pathways. These pathways depend on the relative time ordering of the field interaction events within the experiment. These spectra contain a number of features which we wish to model more effectively: peak positional information and peak broadening. In 2D spectroscopy the broadening is split into homogeneous and inhomogeneous components, with the latter being strongly dependent on the environment. Current projects involve improving models of the inhomogeneous broadening for a range of molecular systems, and investigation of the role of polarisation.

Figure 1: Calculated absorptive 2D spectra for a perylene bisimide vibrionic dimer showing spectral diffusion.

Resonance energy transfer:

Resonance energy transfer (RET, also called fluorescence resonance energy transfer, FRET, or electronic energy transfer, EET) is the process whereby excess energy, from an excited molecule or atom (the donor), is transferred to an acceptor. During RET, all electrons are bound and since their wavefunctions do not overlap, the electrons do not migrate, but the excited state does. RET is mediated by a virtual photon facilitated by dipole-dipole couplings between the donor and acceptor. In our group we model RET using a variety of methods including semi-classical theories (where the electrons are treated quantum mechanically but the fields are treated classically) and quantum electrodynamics (where both matter and fields are treated quantum mechanically). Our current research on RET focuses on understanding quantum effects in RET, such as interferences between different pathways, the role of molecular vibrations and the surrounding environment on RET wavepacket dynamics and in developing new approaches to investigating RET dynamics theoretically, such as using quantum measures to quantify RET behaviour.

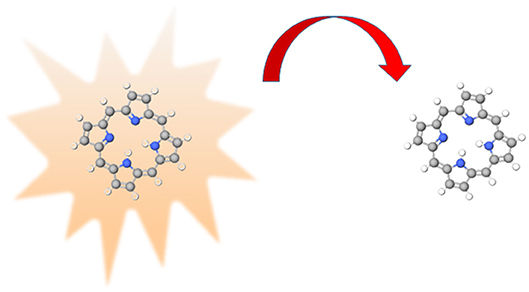
Figure 2: Schematic of resonance energy transfer. The excited donor (on the left-hand side) transfers energy, represented by the red arrow, to the acceptor (on the right).

Quantum behaviour in open systems:

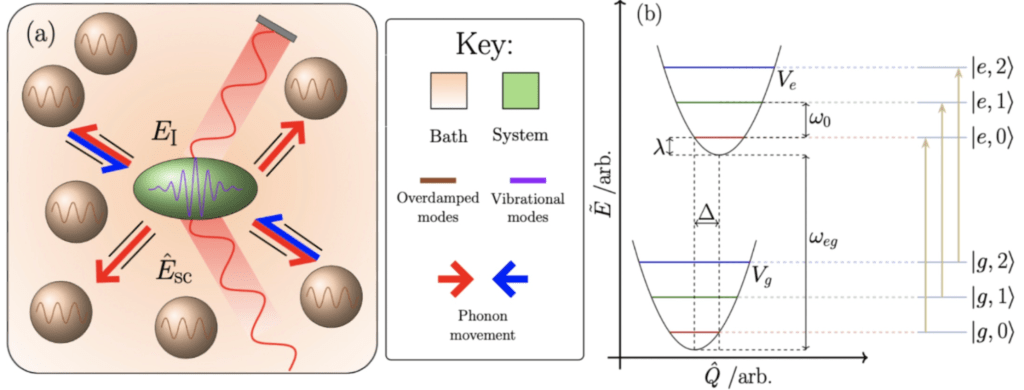
Our recent publication, entitled ‘Phonon signatures in photon correlations’, concerns observing genuine quantum behaviour in a molecular photon counting experiment. We model, through rigorous application of theory, a two level electronic system each with three vibrational levels continuously driven by a laser field which results in emission of a photon beam. We then calculate the detection probability for single photons, and pairs of photons at simultaneous and different times. We show that, through anti-bunching of photon correlation, that genuine quantum effects emerge from the open quantum system. In contrast, we observe more classical bunching behaviour from the phonons. In addition, we consider cross-correlations between the photons and phonons leading to suppression or enhancement of vibrational and electronic signatures.

Figure 3: Schematic of an two electronic level, open quantum system, driven by a continuous laser field.

Quantum information theory:

When a model system of interest is subsumed into an environment we typically use a bilinear coupling to create an interaction between the two. In this scenario quantum channels are established between the two parts of the total system through which bits of quantum information can flow. Quantum information is the complement entropy. This is best explained through the example of pure and mixed states. A pure state has completely distinguishable components: there is maximum information and minimum entropy. In a mixed state, all constituents are indistinguishable from one another, and as such there is a minimum of information and a maximum of entropy. One of our recent projects has involved relating quantum information theory to 2DES through the relationship between inhomogeneous broadening and information. Future projects involve considering flow of physical and ‘virtual’ forms of quantum information within parts of the hierarchical equations of motion.

Modelling with the Feynman and Vernon path integral formalism:

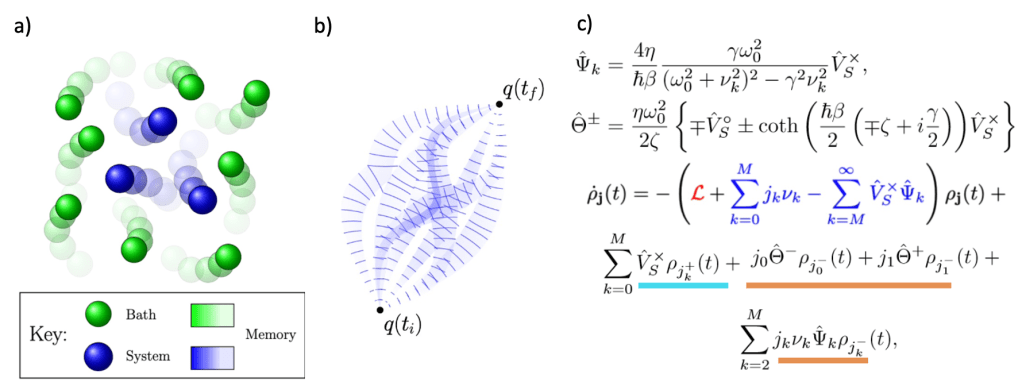
The Feynman and Vernon path integral formalism involves summing up an infinite number of trajectories, or histories, in order to produce a quantum amplitude. The stochastic implications of the procedure make it particularly amenable to use on systems coupled to a large environment ensemble. With this method we are able to compute a system-environment memory term which describes how past states of the system may be able to feedback and alter future states resulting in non-Markovianity. In particular, our work has focused on the hierarchical equations of motion (HEOM) of Tanimura and Kubo (1989). This is an equation derived through the path integral of the density matrix, containing the system-bath influence functional, which incorporates non-Markovian memory effects into the dynamics of a molecular system. We aim to tackle fundamental questions such as: what is the impact on the open quantum system dynamics of movement of the system-environment boundary?